
Candy Necklace exists to demonstrate some connection game principles. (And conversely, the principles
themselves comprise a game.) Candy Necklace may not be a game that anyone would ever want to play, although
there's nothing stopping you.
Candy Necklace has a sister game, Naked Diagonal, which also explores properties of connection games.
In a typical, square-grid connection game, the north and south edges would be colored red, the
east and west edges colored blue. Red's goal would be to connect the red edges with an orthogonally (horizontally
or vertically, or both) interconnected path of red stones. Blue's goal would be to connect the blue edges.
The crosscut is a formation that can bedevil such a game (see the first figure below). If a crosscut is formed,
it could simultaneously prevent both Red and Blue from forming a winning path.
You can't just ban crosscuts. There may come a point in the game where all available placements by both players
form crosscuts.
A crosscut-equivalent loop (explored in detail below) is a loop that can't be filled in without forming a crosscut.
If a crosscut-equivalent loop forms, then (if the loop fills in) a crosscut will form.
If a crosscut-equivalent loop never forms, then a crosscut will never form.
Players are not allowed to form a crosscut-equivalent loop or a crosscut (which is itself a crosscut-equivalent loop).
One of the two players will always have a placement
available. No crosscuts will form, and one of the
players will complete a winning path of stones.
What follows is a discussion of some properties of crosscut-equivalent loops and a means of quickly identifying
crosscut-equivalent loops.
Candy Necklace is a two-player game. A square board of any size is used. The north and
south board edges are colored red. The west and east edges are colored blue. The board is
initially empty.
The two players, Red and Blue, take turns placing their own stones onto unoccupied points on the
board, one stone per turn, starting with Red. Passing is not allowed, but if you don't have an available
placement, your turn is skipped. See PLACEMENT RESTRICTIONS below.
Red must form an orthogonally interconnected path of red stones connecting
the two red board edges. Blue must connect the two blue edges.
A crosscut is comprised of four stones, two of each color. Each stone is orthogonally (horizontally or
vertically) adjacent to its two enemy stones. The following figure shows the two possible crosscut formations.

A "loop" here is a closed path of stones, of either or both colors, interconnected via orthogonal
or diagonal adjacencies, or both. All loops considered here have alternating color stones. Every stone
in the loop is the opposite color of its two neighboring stones. The following figure shows an example of a loop.
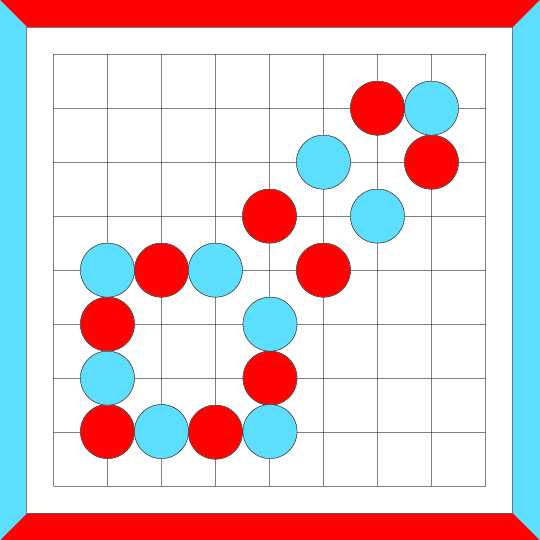
A "crosscut-equivalent" loop can't be filled in without creating a crosscut.
Players are not allowed to form a crosscut-equivalent loop. [There could also be a rule for not allowing
a crosscut, even though a crosscut is itself already a crosscut-equivalent loop. A crosscut is easy to
spot, and doing so can shortcut position evaluations.]
Every crosscut-equivalent loop can be built up from crosscuts in the following manner. Start with
two separate crosscut formations. Remove a stone from each of them, of opposite colors. Then merge the two broken
crosscuts, making them intersect where their missing stones were, as shown in the following figures.

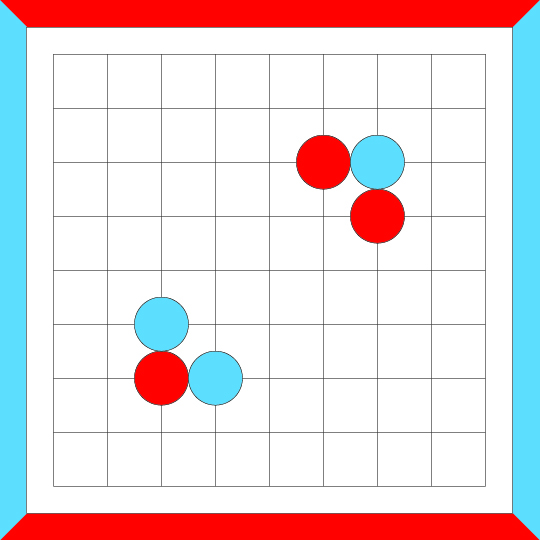

Every crosscut equivalent loop can be built up by repeatedly merging crosscuts into what
started as another crosscut, but has now grown to become a complex loop. An example follows.
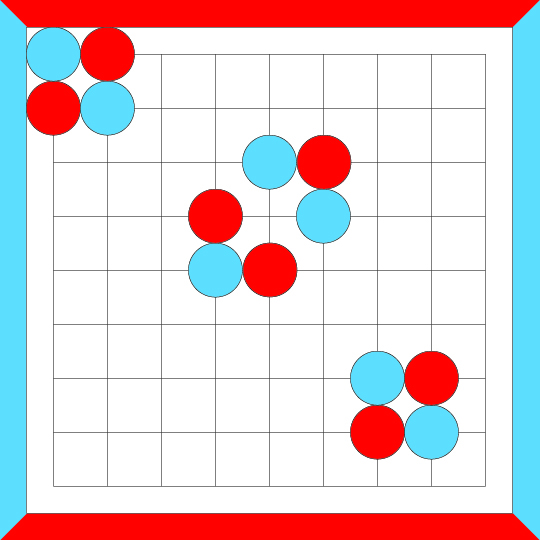

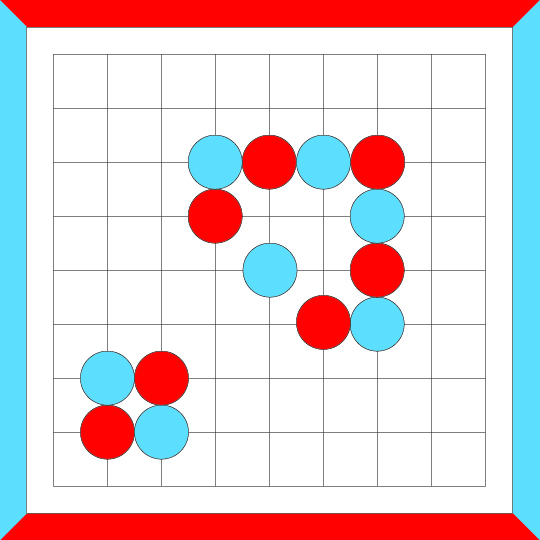
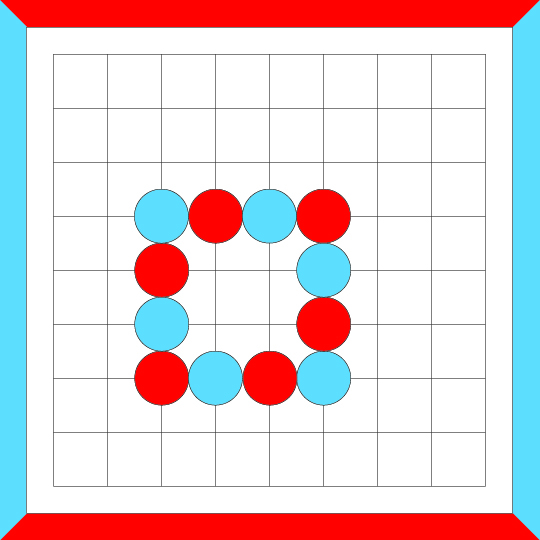
Another series of crosscut merges...
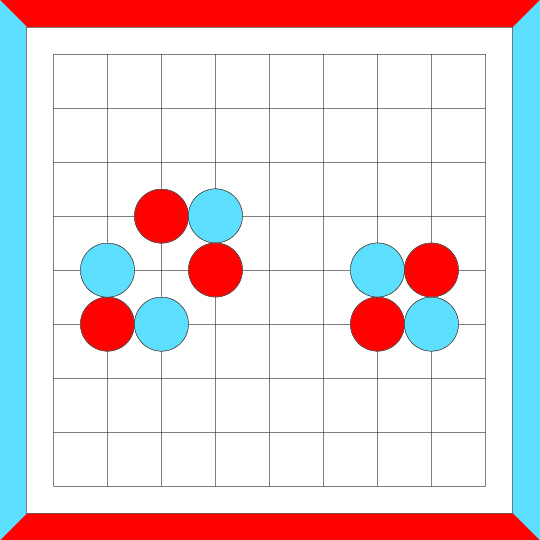
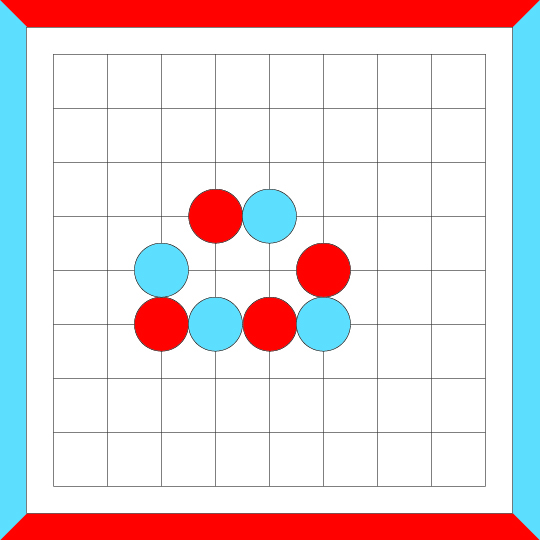
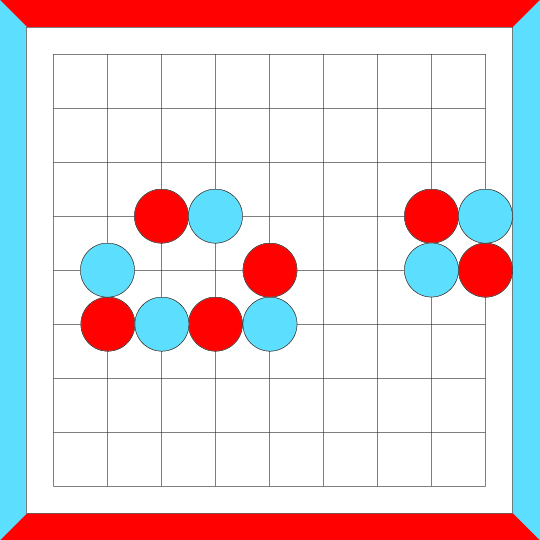
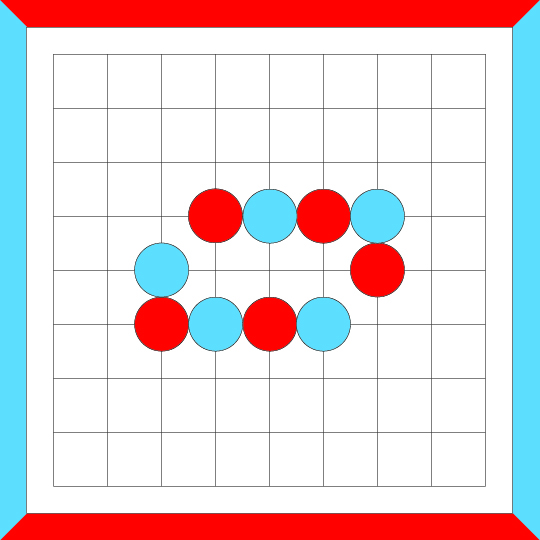


And one more series of crosscut merges...
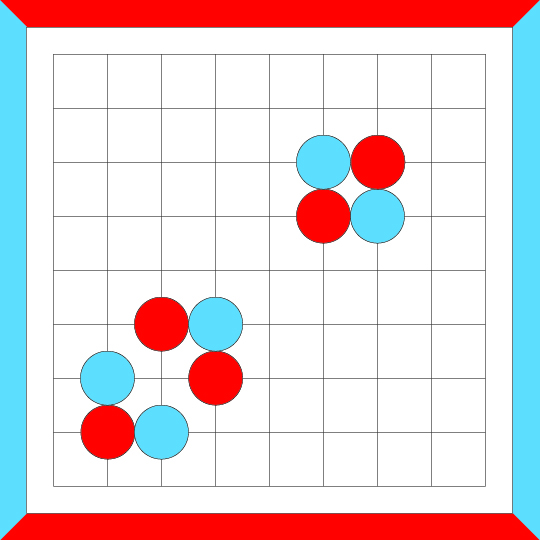
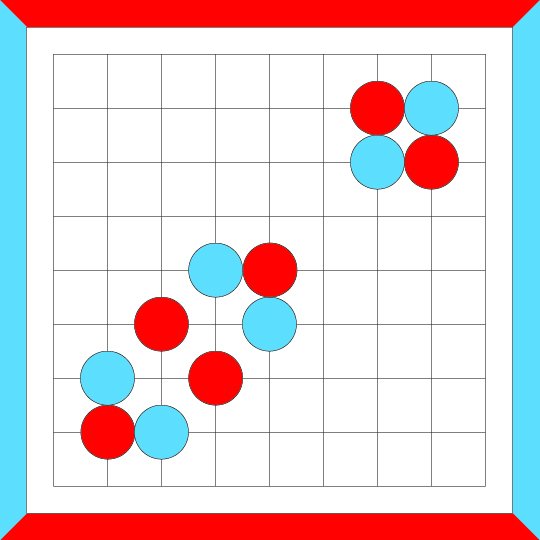
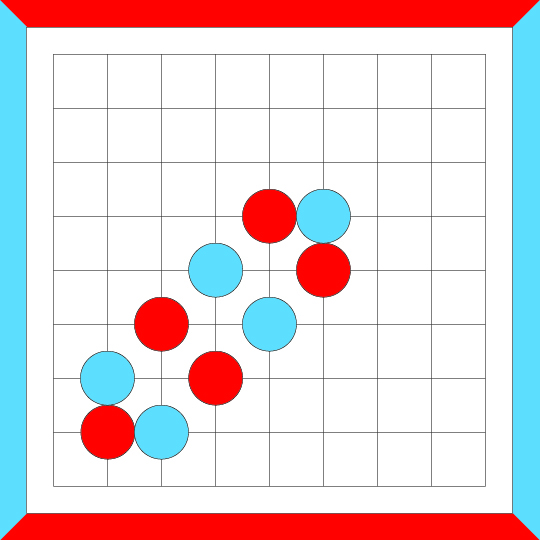
If a loop can be built up by a series of crosscut merges, then the loop is crosscut-equivalent.
If a loop can't be built up by a series of crosscut merges, then the loop is not crosscut-equivalent.
Any crosscut-equivalent loop can be merged with any other crosscut-equivalent loop (by removing one stone
from each loop and joining the two broken loops, as explained above) to form a larger crosscut-equivalent loop.
If a loop can be formed by merging crosscut-equivalent loops, then the loop will itself be crosscut-equivalent.
Here's an example of that...


Loops can be deconstructed with an "unmerging" process - the reverse of the merging process.
Individual crosscut formations are produced as a byproduct of the unmerging process.
The following example demonstrates the unmerge operation.
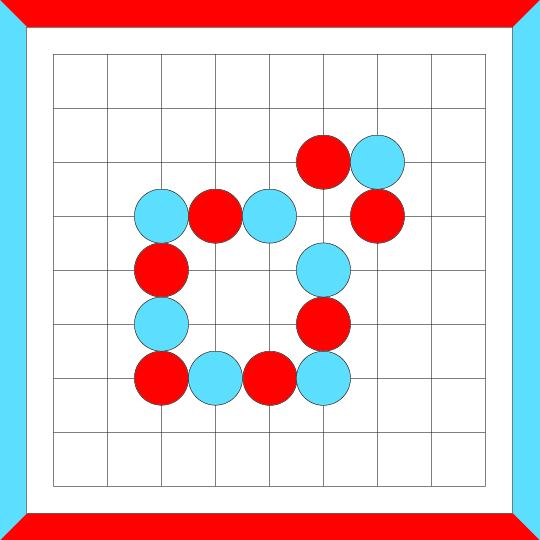
If a loop can be reduced to separate crosscut formations, by applying a series of unmerging operations, then the loop is crosscut-equivalent.
If a loop can't be reduced to separate crosscut formations, by applying a series of unmerging operations, then the loop is not crosscut-equivalent.
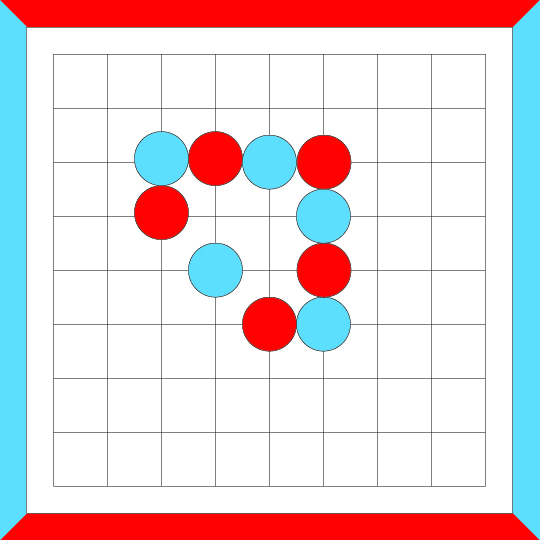
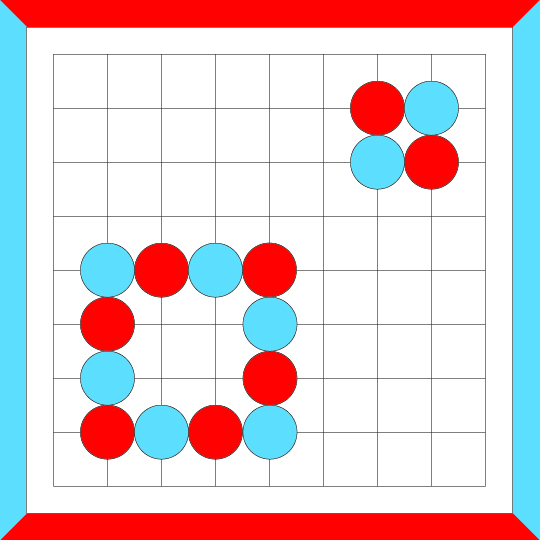
In the following example, the loop cannot be successively unmerged to form nothing but individual crosscut formations.
So the original loop is not crosscut-equivalent.

Evaluating loops by unmerging them could be cumbersome. A quicker way to evaluate loops is needed.
EMPTY AREA - Orthogonally interconnected, maximally inclusive group of unoccupied points.
EMPTY PATH - Empty area in the shape of a single width path.
COMPONENT - A loop may surround a number of empty areas. Each loop portion that surrounds an empty area is
a component.
If a loop's components all meet the following requirements, then the loop is crosscut-equivalent.
If any of the loop's components do not meet the requirements, then the loop is not crosscut-equivalent.
[This is conjecture. It fits all of the loops I've come across so far.]
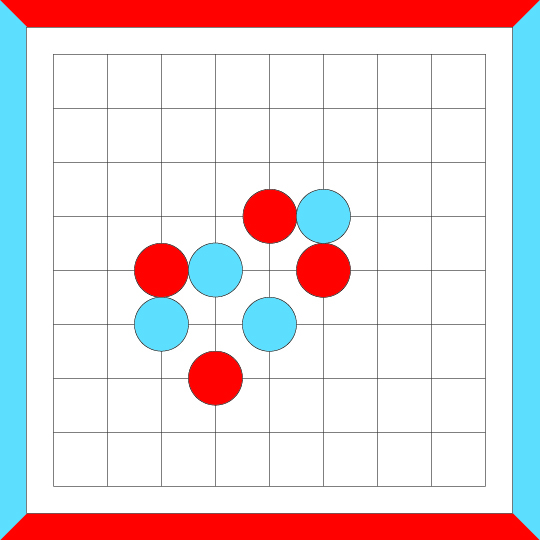
A surrounded, empty area can only be an empty path or a 2x2 area.
The following loop would be disqualified as crosscut-equivalent just based on that.
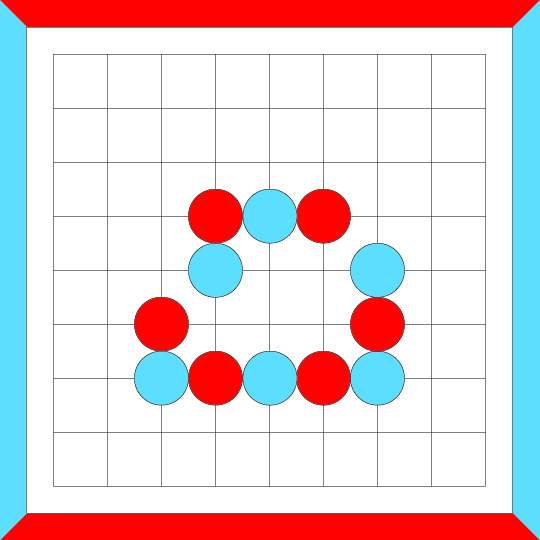
EMPTY PATH
For a surrounded empty path, every stone in the component must be orthogonally across the empty path
from an enemy stone.
The following loop is not crosscut-equivalent because there are like-colored stones
across from each other.

2X2 AREA
For a surrounded 2x2 area,
A. Every stone in the component must be orthogonally across the 2x2 area from an enemy stone.
B. Every point of the 2x2 area must be orthogonally adjacent to two like-colored stones.
The following loop is crosscut-equivalent because both of its components meet the requirements.

The following loop is not crosscut-equivalent because the top-right component doesn't qualify. There
are like-colored stones across from each other, and not every point in its 2x2 area is orthogonally
adjacent to two like-colored stones.

The following loop is not crosscut-equivalent because the top component doesn't qualify. It's too big.
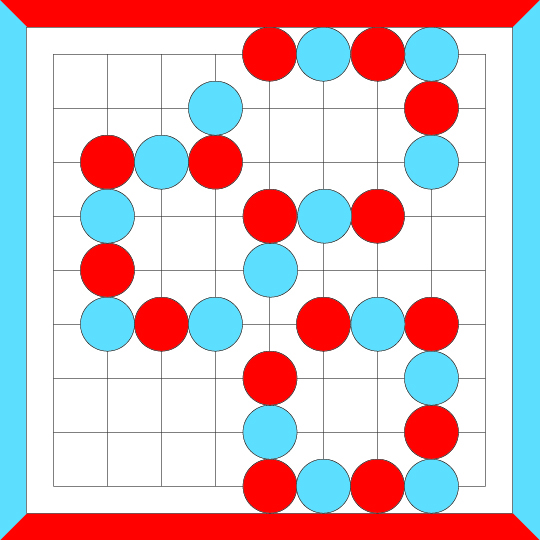
The following loop is not crosscut-equivalent because not every point in the 2x2 area is orthogonally
adjacent to two like-colored stones.

Feel free to publish this rule sheet, and to program the
game of Candy Necklace for online or offline play. No licensing fee or royalties are
expected. However please donít change the name or the rules, and please
attribute the game to me, Mark Steere. My other games can be found at
Mark Steere Games.